C Program For Secant Method With Output

Posted on by

C program for secant method to find roots of polynomial. Write a program to find the real roots of the following equation using the Secant method: f (x) = 23x^4 -13x^3 + 3x^2 - 5x + 38. Let h = r (i) - r (i-1), where r (i) is the root computed in iteration i of your program. Your program should continue to refine its answer until h. In the above code snippet, Fd denotes the Derivative of the Function F. Same approach for solving the quation F(x) = 0. This method is almost identical with Newton's Method except the fact that we choose two initial approximations instead ofone before we start the Iteration Process.

  • Trending Categories
  • Selected Reading
Data StructureMathematical ProblemsAlgorithms

Secant method is also used to solve non-linear equations. This method is similar to the Newton-Raphson method, but here we do not need to find the differentiation of the function f(x). Only using f(x), we can find f’(x) numerically by using Newton’s Divide difference formula. From the Newton-Raphson formula,

Program

we know that,

Now, using divide difference formula, we get,

By replacing the f’(x) of Newton-Raphson formula by the new f’(x), we can find the secant formula to solve non-linear equations.

Note: For this method, we need any two initial guess to start finding the root of non-linear equations.

Input and Output

Algorithm

Input: Two initial guess for root.

Output: The approximate root of a non-linear equation f(x).

C Program For Secant Method With Output Data

Example

C program for secant method with output number

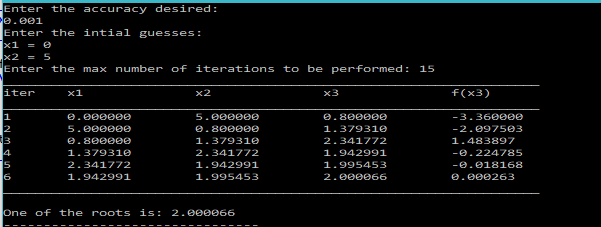
Output

  • Related Questions & Answers
  • Trending Categories
  • Selected Reading

We are given with a function f(x) on a floating number x and we can have three initial guesses for the root of the function. The task is to find the root of the function where f(x) can be any algebraic or transcendental function.

What is Muller Method?

Muller method was first presented by David E. Muller in 1956. A Muller’s method is root finding algorithm which starts with three initial approximations to find the root and then join them with a second degree polynomial (a parabola), then the quadratic formula is used to find a root of the quadratic for the next approximation. That is if x0, x1 and x 2 are the initial approximations then x3 is obtained by solving the quadratic which is obtained by means of x0, x 1 and x2. Then two values among x0, x1 and x2 which are close to x3 are chosen for the next iteration.

Docker for mac raw format. Benefit of learning Muller method?

C program for secant method with output number

Muller method, is one of the root-finding method like bisection method, Regula-Flasi Method, Secant Method etc. having advantages such as −

  • The rate of convergence in Muller method is higher than other methods. Rate of convergence in Muller method is 1.84 whereas it is 1.62 in secant and linear method and 1 for both Regula-flasi and bisection method. Rate of convergence is how much we move closer to the root at each step. So, Muller Method is faster.
  • As it is slower than Newton-Raphson, which has rate of convergence of 2, but the computation of derivate at each step is better in Muller method.Hence, Muller Method is an efficient method.

Working of Muller Method −

  • Let us assume three distinct initial roots x0, x1 and x2.
  • Now draw a parabola, through the values of function f(x) for the points- x0, x1 and x2.

The equation of the parabola, p(x), will be−

p(x )=c+b( x – x 2)+a ( x – x2)2; where a, b and c are the constants.

  • Now, find the intersection of the parabola with the x-axis like x3.
  • How to find the intersection of parabola with the x-axis i.e. x3 −

    • Finding x3, the root of p(x), where, p (x ) = c+b ( x – x 2)+a ( x – x2)2 such that p(x3) = c+b( x3 – x 2)+a ( x3 – x2)2 = 0, apply the quadratic formula to p(x). As we have to take that one which is closer to x2 from the 2 roots, we will use the equation −

      $$X_{3}-X_{2} = frac{-2c}{bpmsqrt{b^{2}-4ac}}$$

      now, as the p(x) should be closer to x2, so we will take that value whose denominator is greater out of two from the above equation.

    • To find a, b and c for the above equation, put x in p(x) as x0, x1, x2 and let these values be p(x0), p(x1) and p(x2) which will be as follows −

      p (x 0) = c+b ( x0 – x 2)+a ( x0 – x2)2 = f ( x0) p ( x1) = c+b (x 1 – x2)+a( x 1 – x2)2 = f ( x1)p(x 2) = c+b( x 2– x2) + a( x 2–x2)2 = c = f ( x2)

    • So, we have three equations for the three variables-a, b and c.

      Now put the following expressions for the x3-x2 and obtain the root of p(x) = x3.

  • If x3 is very much closer to x2 then x3 becomes the root of f(x), else repeat the process of finding the next x3, form the previous x1, x2, x3 as the new x0, x1, x2.

Example

C Program For Secant Method With Output Function

Algorithm

Example

C Program For Secant Method With Output

Output

  • Related Questions & Answers